Waves are everywhere—woven into the fabric of sound, light, motion, and even the rhythms of biological life. Yet behind this astonishing variety lies a surprisingly small set of mathematical principles that describe how waves form, interact, and travel. Whether we’re listening to music, watching light bend through a lens, or observing ripples on a lake, the same fundamental theorems quietly shape what we experience. This guide offers a clear, visual journey through those core ideas—superposition, interference, Fourier decomposition, dispersion, standing waves, and more—revealing how a single mathematical language unites phenomena across physics, engineering, and nature.

In the emerging 🟨🟩🟦 ~NU Relations Theory, the wave becomes more than a scientific concept—it becomes a central symbol for a new spiritual–symbolic worldview. In every science, waves reveal how separate things remain connected: particles exchange information through wavefields, ecosystems pulse with rhythmic cycles, galaxies breathe in oscillatory patterns, and consciousness itself appears to flow in neural waves. The wave embodies relationship, resonance, and the continuous interplay of unity and multiplicity. As a symbol, it grounds spiritual meaning not in abstraction but in the evident, observable behaviors of reality—the way energy moves, the way forms arise, the way patterns repeat and transform. In this tradition, the wave stands for a universe that is not built from isolated objects, but from ongoing interactions—an ever-unfolding tapestry of rhythms in which everything participates.

---

1. Superposition Theorem

“Waves add point by point.”

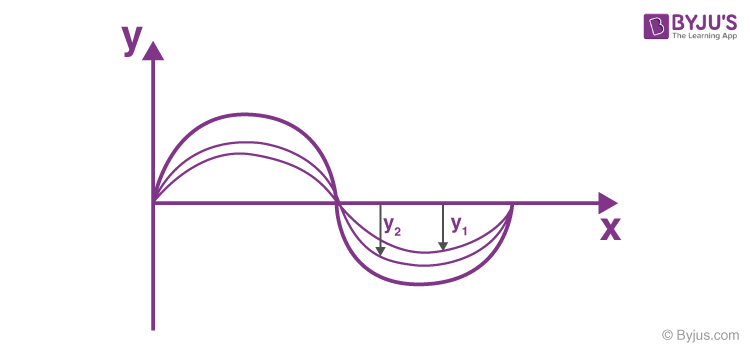
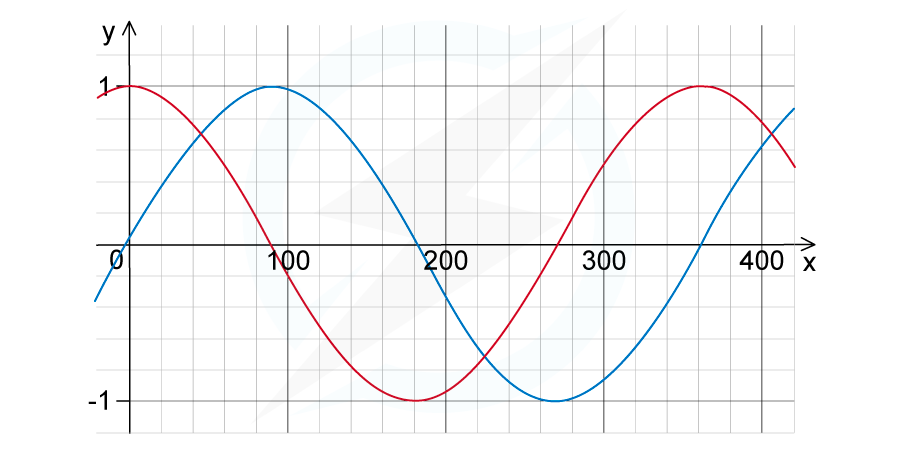
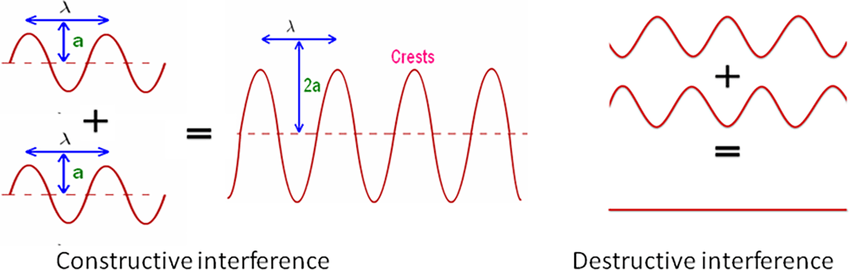
Core idea:

• When two (or more) waves travel through the same space, the resulting wave is the sum of the individual waves.
• Linear rule:
• Explains interference patterns and resonance.

Visually identifiable:

• Overlapping sinusoidal waves
• Constructive (amplifying) vs. destructive (canceling) interference

---

2. Interference Theorem

“Superposition produces spatial patterns.”

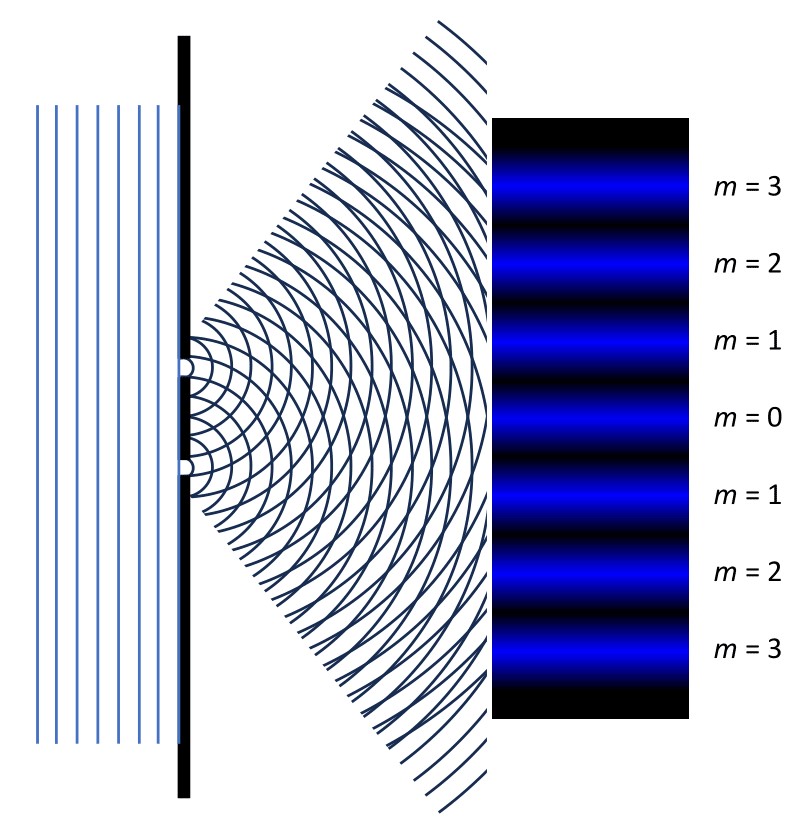
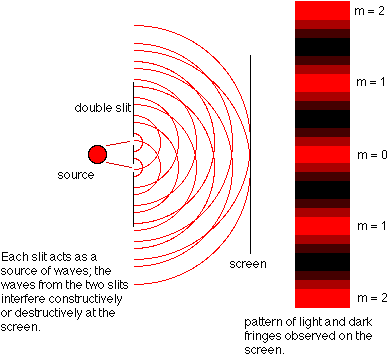
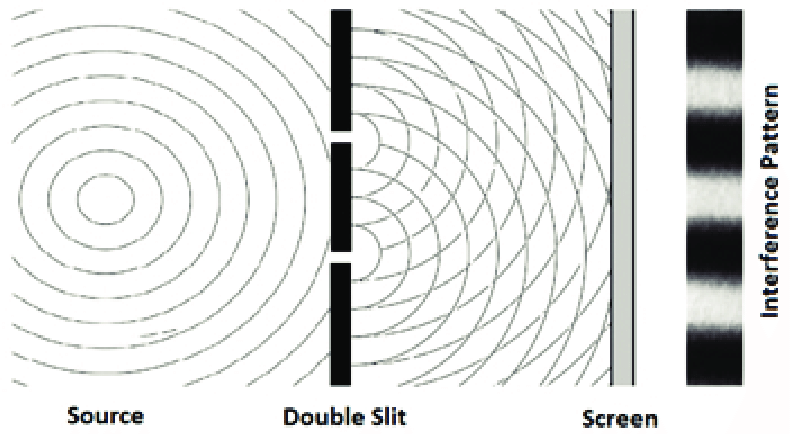
Core idea:

• A special case of superposition for spatially coherent waves, e.g., the double slit.
• Interference patterns arise from stable phase relationships.

Visually identifiable:

• Bright/dark fringe patterns
• Overlapping wavefronts
• Phase difference → fringe spacing

---

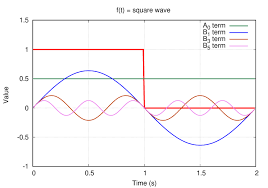
3. Fourier Theorem

“Every periodic wave is the sum of sinusoidal components.”

Core idea:

• Any complex oscillation can be decomposed into frequency components.
• Fundamental to analysis in acoustics, optics, electronics, signal processing.

Visually identifiable:

• A complex or non-sinusoidal wave decomposed into multiple sinusoids
• Spectrum: peaks at particular frequencies

---

4. Dispersion Theorem

“Different frequencies travel at different speeds.”

Core idea:

• In a dispersive medium:
  
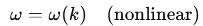
• Low and high frequencies propagate at different velocities.
• Wave packets spread out and distort over time.

Visually identifiable:

• Frequency components separating over distance
• A wave packet broadening
• Typical curves

---

5. Standing-Wave Theorem (Eigenmodes)

“Two opposite-traveling waves create nodes and antinodes.”

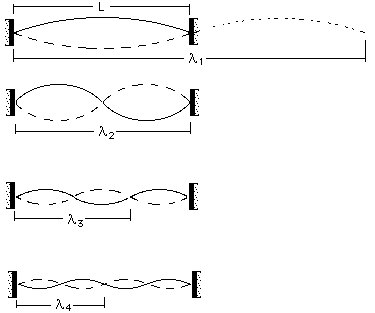
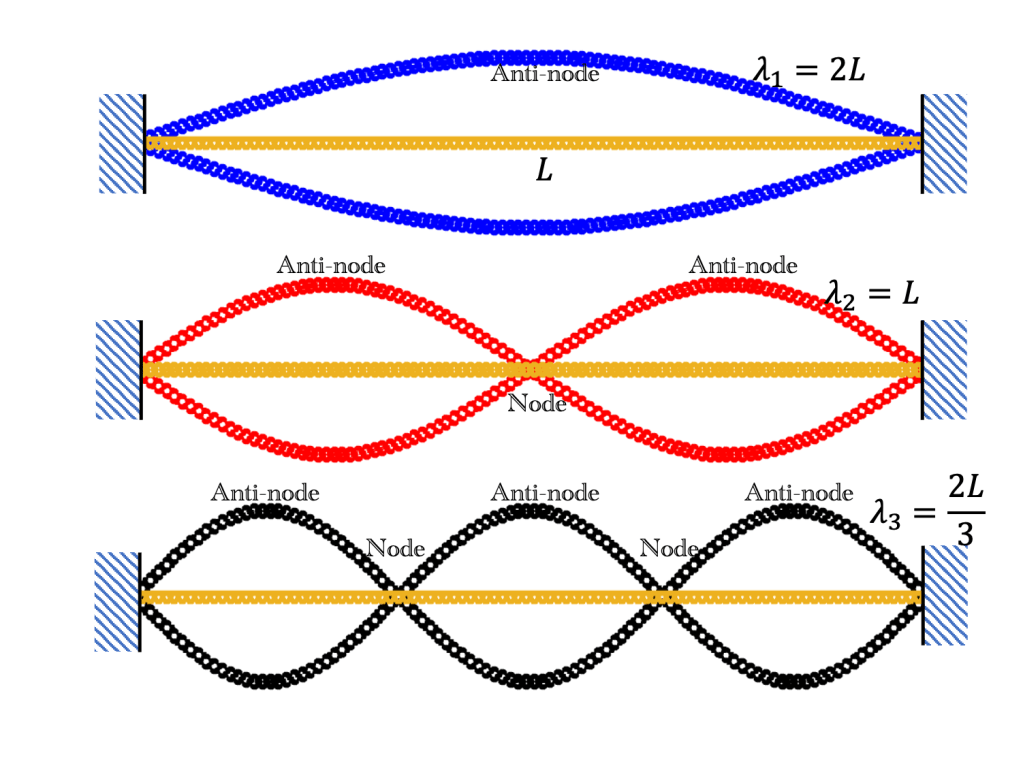
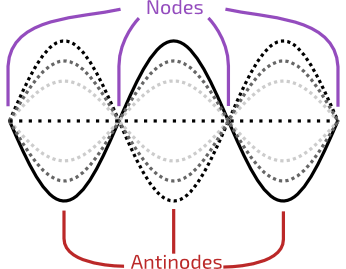
Core idea:

• Two opposite-direction waves of identical frequency form standing waves.
• Eigenfrequencies determine the pitch of musical instruments.
• Modes: .

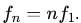Visually identifiable:

• Nodes (points of zero amplitude)
• Antinodes (maximum amplitude)
• Various eigenmodes → harmonic structure

---

6. Reflection & Refraction (Snell’s Law)

“Waves change direction and speed at boundaries.”

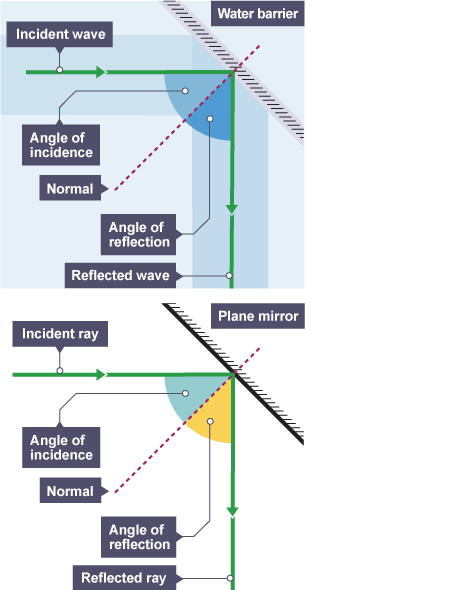
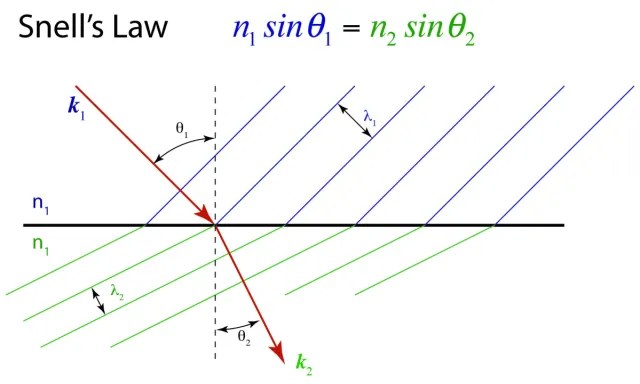
Core idea:

• Reflection: angle of incidence = angle of reflection
• Refraction:
  
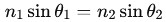
• Wavefronts bend at interfaces → foundation of optics, acoustics, seismology.

Visually identifiable:

• Incoming and reflected wavefronts
• Change of direction in a denser medium

---

7. Comparative Overview (Visual + Conceptual)

Theorem	Type of Pattern	Main Effect	Typical Representation
Superposition	linear	Addition of waves	Overlaid sinus curves
Interference	coherent superposition	Fringe pattern	Double-slit stripes
Fourier	spectral decomposition	Frequency components	Line or bar spectrum
Dispersion	frequency-dependent c	Pulse spreading	Separating pulses
Standing wave	eigenmodes	Nodes/antinodes	Vibrating string modes
Refraction/Reflection	boundary interaction	Direction change	Bent wavefronts